Adding Functions to the Calculator

Añadiendo funciones a la calculadora

Queremos extender nuestra calculadora para que soporte funciones con una sintáxis como la de este ejemplo:

x = 10,     # This x is global
f = fun (a) {
  x = a+2i, # This x is local
  3i*x      # returned value
},
b = f(4),
print(b), # -6+12i
print(x)  # 10

Vamos a hacerlo teniendo en cuenta las siguientes consideraciones:

1. Limitaremos las funciones a que reciban 0 o 1 parámetros
2. El cuerpo de la función es una expresión entre llaves { e }
3. Las funciones retornan el valor evaluado para e.
4. Las funciones crean un nuevo ámbito: tanto los parámetros como las variables iniciadas dentro de la expresión de una función serán locales a la función
5. Tan pronto una variable es inicializada dentro del cuerpo de una función se la considera declarada y es local a la función (parecido a como se hace en Ruby)
6. Nuestras funciones son anónimas

Cuando se llame a nuestro transpiler con la entrada anterior, se debe generar un programa JS equivalente a este:

✗ bin/calc2js.mjs test/data/input/test-fun-scop2.calc
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $x, $f, $b;
 
(
  (
    (
      $x = Complex("10"), 
      $f = function($a) {
        let $x;
        return $x = $a.add(Complex("2i")), 
          Complex("3i").mul($x);
      }
    ), 
    $b = $f(Complex("4"))
  ), 
  print($b)
), 
print($x);

Las funciones son expresiones

Funciones que retornan funciones

Las funciones que introduzca podrán recibir como argumento una función y también pueden retornar funciones. En el siguiente ejemplo sum es una función que retorna una función:

sum = fun (n) {
  fun(x) { n+x } 
},
r = sum(4)(5),
print(r) # 9

cuya traducción podría ser:

➜  functions-solution git:(functions) ✗ bin/calc2js.mjs test/data/input/test-fun3.calc              
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $sum, $r;
 
(
  $sum = function($n) {
    return function($x) {
        return $n.add($x);
    };
  }, 
  $r = $sum(Complex("4"))(Complex("5"))
), 
print($r);

Funciones que reciben funciones y retornan funciones

En este otro ejemplo, la función add recibe una función f y retorna otra función que a su vez espera como argumento otra función g la cual retorna una función que es la función que suma a su argumento x los valores de la primera f(x) y la segunda g(x):

add = fun(f) {
  fun(g) { 
    fun(x) { 
      f(x)+g(x) 
    } 
  }
},
square = fun(x) { x*x },
double = fun(x) { 2*x },
print(add(square)(double)(4)) # 24+0i

Cuando la compilamos

✗ bin/calc2js.mjs test/data/input/test-fun4.calc         
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $add, $square, $double;
 
(
  (
    $add = function($f) {
      return function($g) {
        return function($x) {
            return $f($x).add($g($x));
        };
      };
    }, 
    $square = function($x) {
      return $x.mul($x);
    }
  ), 
  $double = function($x) {
    return Complex("2").mul($x);
  }
), 
print($add($square)($double)(Complex("4")));

y cuando la ejecutamos obtenemos:

✗ bin/calc2js.mjs test/data/input/test-fun4.calc | node -
{ re: 24, im: 0 }

Encadenamiento de llamadas

Comentarios

Como se ve en los ejemplos anteriores se deberán admitir comentarios de una línea que van desde la aparición del carácter # hasta el final de la línea. Soporte también comentarios multilínea a la manera de JavaScript: /* ... */.

Operadores Lógicos y de Comparación

Añada operadores lógicos

• && para el and lógico,
• || para el or lógico y
• el prefijo ! para el not
• además de los valores truey false

Short Circuit Evaluation and if then else

La interpretación de estos operadores se hará como en JavaScript: valores distintos de cero en un contexto lógico se evaluan a true, etc. Además las evaluaciones se harán en circuito corto (short-circuit) de manera que el siguiente programa calcula el factorial de un número natural:

fact = fun(n) {
  !(n == 0) && n * fact(n - 1) || 1
},
print(fact(5))

Que cuando se compile dará:

✗ bin/calc2js.mjs test/data/input/test-recursive2.calc         
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $fact;
 
$fact = function($n) {
    return !$n.equals(Complex("0")) 
      && $n.mul($fact($n.sub(Complex("1"))))
      || Complex("1");
}, 
print($fact(Complex("5")));

y cuando se ejecute dará:

✗ bin/calc2js.mjs test/data/input/test-recursive2.calc | node -
{ re: 120, im: 0 }

Type Handling in Dynamic Languages

Type checking is the process of verifying and enforcing constraints of types in values. The language type-checker determines whether these values are used appropriately or not.

For each operation, there are numerous possible type combinations and decisions need to be made about them.

In either case, a guidance error message should be issued for any operation that is decided not to be supported.

Type Checking: Basic concepts

For an introduction to the basic concepts on type checking see the section Type Checking: Basic Concepts

Function Arithmetic

For example, we might decide to generalize to support arithmetic operations on functions whenever they make sense, so that a program like this:

f = fun(x) { 2*x },
g = fun(x) { 3*x },
r = fun(y) { 3*y },
h = g + f,
k = g * f,
e = g == r,
print(h(1+i)), # 5 + 5i
print(k(2-i)), # 18 - 24i
print(e(1))  # true

To achieve that we would need to extend the arithmetic operations to JS functions. Something like this:

let Operators = {
  add: '+',  mul: '*',  div: '/',  equals: '==',  pow: '**',  neg: '-' // ... etc.
};
 
for (let op in Operators) {
  Boolean.prototype[op] = function (other) { /* ... */   };
  Function.prototype[op] = function (other) {
    switch (typeof other) {
      case 'boolean':  return (...x) => this(...x)[op](Number(other))
      case 'object': /* ... */
      case 'function':
        try {
          return (...x) => this(...x)[op](other(...x))
        } catch (e) {
          throw new Error(`Unsupported ${op} for function ${other}`)
        }
      default:
        throw new Error(`Unsupported ${op} for type ${typeof other}`)
    }
  }
}

will work resulting in an execution like this:

➜ bin/calc2js.mjs test/data/input/test-fun-add.calc | do not give -
{ re: 5, im: 5 }
{ re: 18, im: -24 }
true

See section Rank Polymorphism

Arithmetic of Functions and numbers

But we may also want to allow functions to be operated on numbers (by extending a number as the function constant on that number):

f = fun(x) { 2*x },
h = f + 3, # 3 is the constant function f(x) = 3 for all x
print(h(1+i)) # 5 + 2i

which would be interpreted as:

let Operators = {
  add: '+',  mul: '*',  div: '/',  equals: '==',  pow: '**',  neg: '-' // ... etc.
};
 
for (let op in Operators) {
  Boolean.prototype[op] = function (other) { /* ... */   };
  Function.prototype[op] = function (other) {
    switch (typeof other) {
      case 'boolean':  return (...x) => this(...x)[op](Number(other))
      case 'object': if (other instanceof Complex) {
            return (...x) => this(...x)[op](other)
        }  else { throw new Error(`Unsupported ${op} for ${other}`) }
      case 'function': /* ... */
      default:
        throw new Error(`Unsupported ${op} for type ${typeof other}`)
    }
  }
}

That would give rise to the following execution:

  ✗ bin/calc2js.mjs test/data/input/test-fun-add1.calc | node -
{ re: 5, im: 2 }

Arithmetic of Functions and Booleans

It would also be possible to extend addition/subtraction etc. to a function with a boolean.

One possible interpretation would be to promote the boolean value true to 1+0i and false to 0:

f = fun(x) { 2*x },
h = f + true,
print(h(1+i)) # 3 + 2i

That implies extending the arithmetic operations to functions and booleans:

Function.prototype[op] = function (other) {
    switch (typeof other) {
      case 'boolean':
        return (...x) => this(...x)[op](Number(other))
      /* ... */
    }
}

The former input is compiled to:

➜  functions-solution git:(functions) ✗ bin/calc2js.mjs test/data/input/test-fun-add2.calc         
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
/* End of support code */
let $f, $h;
(
  $f = function($x) {
    return Complex("2").mul($x);
  }, 
  $h = $f.add(true)
), 
print(
  $h(Complex("1").add(Complex("i")))
);

which when executed gives:

✗ bin/calc2js.mjs test/data/input/test-fun-add2.calc | node -
{ re: 3, im: 2 }

Type Promotion

For instance, considere the following example:

f = fun(x) { fun(y) { x+y} },
print((f+2)(3)(5)) # 10

When compiled we have to produce something like this translation:

➜  functions-solution git:(functions) ✗ bin/calc2js.mjs test/data/input/test-fun-call2.calc         
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $f;
 
$f = function($x) {
    return function($y) {
        return $x.add($y);
    };
}, 
print(
  $f.add(Complex("2"))(Complex("3"))(Complex("5"))
);

Notice how the function $f has now a method add that is called with argument Complex(2). The run time library support is inserting this new behavior to the funcion $f. it can be considered an example of Duck Typing.

Duck Typing

this way, via the run time support injecting behavior as .add to the functions objects we can make the JS interpreter to produce this output:

➜  functions-solution git:(functions) ✗ bin/calc2js.mjs test/data/input/test-fun-call2.calc | node -
{ re: 10, im: 0 }
➜  functions-solution git:(functions) ✗ 

Language Symmetry

This implies that if we add the add method to the Functions so that it takes a complex number as an argument SomeFunction.add(someComplexNumber) should also be extended to add for complex numbers to support functions as arguments someCompleNumber.add(SomeFunction).

That is, if we consider the symmetric of the former example with 2+f instead of f+2 it has to work the same way:

f = fun(x) { fun(y) { x+y} },
print((2+f)(3)(5)) # 10

The translation produces a memberExpression Complex("2").add($f):

➜  functions-solution git:(extendedcalls) ✗ bin/calc2js.mjs test/data/input/test-fun-call2-symmetric.calc        
#!/usr/bin/env node
const Complex = require("/Users/casianorodriguezleon/campus-virtual/2223/pl2223/practicas/functions/functions-solution/src/complex.js");  
const print = x => { console.log(x); return x; };
let $f;
 
$f = function($x) {
    return function($y) {
        return $x.add($y);
    };
}, 
print(
  Complex("2").add($f)(Complex("3"))(Complex("5"))
);

If we extend the behavior of Complex appropriately it can work:

➜  functions-solution git:(extendedcalls) ✗ bin/calc2js.mjs test/data/input/test-fun-call2-symmetric.calc | node -
{ re: 10, im: 0 }

Be bold in your designs but keep them simple.

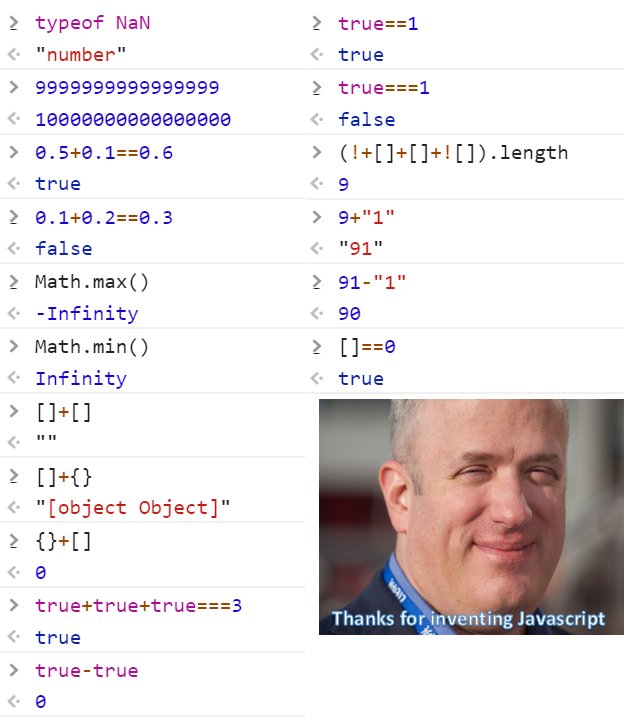
Allowing too much freedom and inconsistent decisions may produce surprising results. JS is quite famous for this:

(opens in a new tab)

For example, we could decide that two logical values can be checked for equal but cannot be added, so this program:

b = false == false,
print(b), #true
c = true + true # error

would result in output like this:

✗ bin/calc2js.mjs test/data/input/test-logic2.calc | do not give -
true
Error. Unsupported operator "+" for type boolean

In this lab, the decision to adopt on the combinations of operations and types is left to your discretion, such as: Do we admit adding a function and a Boolean and produce a result or, on the contrary, do we consider it an error? Certain extensions could be the subject for the final TFA.

In any case, remember that you must ensure that the error messages issued must be as explanatory as possible.

Videos

Clase del 06/03/2024. Nested calls. Scope analysis. Extending operations: type management:

Clase del 05/03/2024. Function expressions: syntax and translation. Calls:

Clase del 04/03/2024. Consideraciones de diseño. Sintáxis de las expresiones función:

Clase del 22/03/2023. Hasta el minuto 25 se explica como realizar el examen parcial del curso 22/23. Le será muy útil para preparar examenes. A partir del minuto 25 se explican las bases para la práctica functions:

Clase del 27/03/2023. Se continúa la explicación de como realizar la práctica de funciones:

Clase del 28/03/2023. Análisis de tipos en el lab. Lookup en el scope analysis. Soporte a las operaciones para los nuevos tipos. Nueva sintáxis para las calls:

Vídeos sobre manejo del AST con ast-types

En los próximos cuestionarios se incluirán preguntas sobre el manejo de ast-types. Se recomienda ver los videos que se describen a continuación.

Clase del 13/03/2023. Se describe el soporte de ast-types para el recorrrido y modificación de nodos (Métodos visit):

El vídeo está enfocado a mostrar como usar ast-types en la resolución del problema planteado en la práctica ast types: spread operator (opens in a new tab) desarrollada durante el curso 22/23.

Clase del 08/03/2023. Se describe el soporte para scopes de ast-types:

Smells, The Open Closed Principle, the Switch Smell and the Strategy pattern

See section The Open Closed Principle and the Strategy Pattern

Pruebas, Covering e Integración Continua

Escriba las pruebas, haga un estudio de cubrimiento usando c8 (opens in a new tab) y añada integración continua usando GitHub Actions.

Lea las secciones Testing with Mocha y Jest.

Avoiding the preamble in the tests

In your template for the code generation, use a special string like \n/* End of support code */\n\n to mark the end of the preamble and the beginning of the generated code.

const { {{ dependencies }} } = require("{{root}}/src/support-lib.js");
 
/* End of support code */
 
{{code}}

Then in your tests, use a funtion like the following to remove the preamble by using a regexp that removes from the beginning to the from the generated code:

function removeDependencies(s) {
  const REGULAR_SEPARATION = /^(.|\n)*\n\/\* End of support code \*\/\n\n/
  const pruned = s.replace(REGULAR_SEPARATION, '')
 
  return removeSpaces(pruned);
}

then you can use it in your tests removing the preamble from both the expected and the actual output:

for (let i = 0; i < Test.length; i++) {
  it(`transpile(${Tst[i].input}, ${Tst[i].actualjs}) (No errors: ${Boolean(Tst[i].expectedout)})`, async () => {
    let actualjs = await transpile(Test[i].input, Test[i].actualjs);  
    let expectedjs = fs.readFileSync(Test[i].expectedjs, 'utf-8')
 
    let trimActualJS = removeDependencies(actualjs)
    let trimExpectedJS = removeDependencies(expectedjs)
    assert.equal(trimActualJS, trimExpectedJS);
  });
}

Publishing a package to the GitHub Registry

See the chapter Publishing a package to the GitHub Registry and the sections

• Configure npm
• What are scopes?
• What is Github Registry?
• Other ways to set the Scope (opens in a new tab)

One way to set GitHub as the registry is to add a publishConfig field to your package.json file

{
  "name": "@ull-esit-pl-2324/functions-name-ape1-ape2-aluXXX",
  "version": "1.2.0",
  "description": "A lab for PL. Adding Functions to our Calculator",
  "main": "src/transpile.js",
  "bin": {
    "calc2js": "./bin/calc2js.js"
  },
  "publishConfig": {
    "registry": "https://npm.pkg.github.com"
  },
  ...
}

Documentación

Documente el módulo incorporando un README.md y la documentación de la función exportada usando JsDoc. Lea la sección Documenting the JavaScript Sources

Rubric

functions Repos

References

• COMP442/6421 - Compiler Design - week 8 - AST traversal using the Visitor pattern. Concordia University, Montreal , Canada. 2022
  • 
    
• Compiler Design Module 34 : Semantic Analysis Introduction to Scope. IITI Delhi. Compiler AI Labs. 2020
  • 
    
• Compiler Design Module 35 : Semantic Analysis as Recursive Descent over AST. IITI Delhi. Compiler AI Labs. 2020
  • 
    
• ast-types: See the scope section
• recast

Polymorphism

See the notes by Casiano Rodríguez León. 2011:

1. Sobrecarga, Polimorfismo e Inferencia de Tipos (opens in a new tab)
2. Expresiones de Tipo, Sistemas de Tipos y Comprobadores de Tipos (opens in a new tab)]
3. Equivalencia de Expresiones de Tipo (opens in a new tab)
4. Un Lenguaje con Funciones Polimorfas (opens in a new tab)