Análisis de Tipos: Conceptos Básicos

En la mayoría de los lenguajes los objetos manipulados son declarados en alguna parte del programa y usados en otras. Ya dijimos que el análisis de ámbito es el cálculo de la función que asigna a un uso de un objeto la definición que se le aplica.

El análisis de tipos tiene por objetivo asegurar que el uso de los objetos definidos es correcto: esto es, que su uso se atiene a la semántica de su definición; por ejemplo,

• que un array de enteros no es llamado como función o
• que no se intenta incrementar una función o
• que el valor retornado por una función es de la naturaleza descrita en su definición.

Expresiones de Tipo

Una forma adecuada de representar los tipos dentro de un compilador es usando un lenguaje de expresiones de tipo.

Un lenguaje de las expresiones de tipo debe describir de manera clara y sencilla los tipos del lenguaje fuente. No confunda este lenguaje con el sub-lenguaje del lenguaje fuente que consiste en las declaraciones o definiciones.

No tienen por que ser iguales. El compilador traduce las declaraciones de tipo en expresiones de tipo.

El lenguaje de las expresiones de tipo es la representación interna que el compilador tiene de estas declaraciones y depende del compilador.

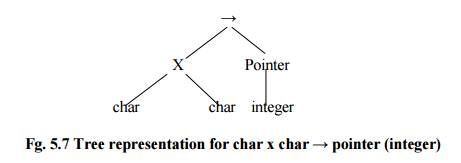
Sistema de Tipos

Un Sistema de Tipos de un lenguaje/compilador es el conjunto de reglas del lenguaje
que permite asignar expresiones de tipo a las instancias de uso de los objetos del programa.

Si bien el sistema de tipos es una propiedad del lenguaje, no es raro que los compiladores introduzcan modificaciones en el sistema de tipos del lenguaje.

Por ejemplo en Pascal el tipo de un array incluye los índices del array. Esto y las reglas de equivalencia de tipos de Pascal limitaban gravemente la genericidad de las funciones en Pascal. Por eso algunos compiladores Pascal permitian en una llamada a función la compatibilidad de tipos entre arrays de diferente tamaño y diferentes conjuntos de índices. Desgraciadamente la forma en la que lo hacían difería de compilador a compilador.

Comprobador de Tipos

Un Comprobador de Tipos verifica que el uso de los objetos en los constructos de uso se atiene a lo especificado en sus declaraciones o definiciones de acuerdo a las reglas especificadas por el sistema de tipos.

Tipado estático y tipado dinámico

Un lenguaje de programación tiene tipado estático si su comprobación de tipos ocurre en tiempo de compilación sin tener que comprobar equivalencias en tiempo de ejecución.

Un lenguaje de programación tiene tipado dinámico si el lenguaje realiza comprobaciones de tipo en tiempo de ejecución.

En un sistema de tipos dinámico los tipos suelen estár asociados con los valores no con las variables.

Tipado Fuerte y Tipado débil

Aunque el significado de los términos Fuertemente Tipado y su contrario Débilmente Tipado varían con los autores, parece haber consenso en que los lenguajes con tipado fuerte suelen reunir alguna de estas características:

• La comprobación en tiempo de compilación de las violaciones de las restricciones impuestas por el sistema de tipos. El compilador asegura que para cualesquiera operaciones los operandos tienen los tipos válidos.

• Toda operación sobre tipos inválidos es rechazada bien en tiempo de compilación o de ejecución.

• Algunos autores consideran que el término implica desactivar cualquier conversión de tipos implícita. Si el programador quiere una conversión deberá explicitarla.

• La ausencia de modos de evadir al sistema de tipos.

• Que el tipo de un objeto de datos no varíe durante la vida del objeto. Por ejemplo, una instancia de una clase no puede ver su clase alterada durante la ejecución.

Sobrecarga, Polimorfismo e Inferencia de Tipos

En algunos lenguajes se permite la sobrecarga de funciones. Así es posible tener dos funciones llamadas min:

  int min(int a, int b) {       string min(string a, string b) {     
       if (a < b) return a;          if (strcmp(a, b) < 0) return a; 
       return b;                     return b;                       
  }                             }                                 

A la hora de evaluar el tipo de las expresiones es el contexto de la llamada el que determina el tipo de la expresión:

    float x,y;
    int a,b;
    string c,d;
 
    u = min(x,y); /* Puede que correcto: x e y seran truncados a enteros. Tipo entero */
    v = min(a,b); /* Correcto: Tipo devuelto es entero */
    w = min(c,d); /* Correcto: Tipo devuelto es string */
    t = min(x,c); /* Error */

¿Como afecta al análisis de ámbito la sobrecarga de operadores?

Inferencia de Tipos

La Inferencia de Tipos hace referencia a aquellos algoritmos que deducen automáticamente en tiempo de compilación - sin información adicional del programador, o bien con anotaciones parciales del programador - el tipo asociado con un uso de un objeto del programa.

Un buen número de lenguajes de programación funcional permiten implantar inferencia de tipos (Haskell, OCaml, ML, etc).

Type inference refers to the process of determining the appropriate types for expressions based on how they are used.

For example, in the expression f 3, OCaml knows that f must be a function, because it is applied to something (not because its name is f!) and that it takes an int as input. It knows nothing about the output type. Therefore the type inference mechanism of OCaml would assign f the type int -> 'a where 'ais a type variable.

    ➜  pl2324-apuntes git:(main) ✗ ocaml
    OCaml version 5.0.0
    Enter #help;; for help.
 
    # fun f -> f 3;;
    - : (int -> 'a) -> 'a = <fun>

Véase como ejemplo de inferencia de tipos la siguiente sesión en Ocaml:

    pl@nereida:~/src/perl/attributegrammar/Language-AttributeGrammar-0.08/examples$ ocaml
            Objective Caml version 3.09.2
 
    # let minimo = fun i j -> if i<j then i else j;;
    val minimo : 'a -> 'a -> 'a = <fun>
    # minimo 2 3;;
    - : int = 2
    # minimo 4.9 5.3;;
    - : float = 4.9
    # minimo "hola" "mundo";;
    - : string = "hola"

El compilador OCaml infiere el tipo de las expresiones.

Así el tipo asociado con la función minimo es 'a -> 'a -> 'a que es una expresión de tipo que contiene variables de tipo. El operador -> es asociativo a derechas y asi la expresión debe ser leída como 'a -> ('a -> 'a).

Básicamente dice: es una función que toma un argumento de tipo 'a (donde 'a es una variable de tipo que será instanciada en el momento del uso de la función) y devuelve una función que toma elementos de tipo 'a y retorna elementos de tipo 'a.

Funciones de Varias Variables versus Funciones que retornan Funciones

Aunque podría pensarse que una descripción mas adecuada del tipo de la función minimo fuera 'a x 'a -> 'a, lo cierto es que en algunos lenguajes funcionales es usual que todas las funciones sean consideradas como funciones de una sóla variable.

La función de dos variables 'a x 'a -> 'a puede verse como una función 'a -> ('a -> 'a).

En efecto la función minimo cuando recibe un argumento retorna una función:

    # let min_mundo = minimo "mundo";;
    val min_mundo : string -> string = <fun>
    # min_mundo "pedro";;
    - : string = "mundo"
    # min_mundo "antonio";;
    - : string = "antonio"
    # min_mundo 4;;
    This expression has type int but is here used with type string
    # min_mundo(string_of_int(4));;
    - : string = "4"

Esta estrategia de reducir funciones de varias variables a funciones de una variable que retornan funciones de una variable se conoce con el nombre de currying o aplicación parcial.

Polimorfismo

El polimorfismo es una propiedad de ciertos lenguajes que permite una interfaz uniforme a diferentes tipos de datos.

Se conoce como función polimorfa a una función que puede ser aplicada o evaluada sobre diferentes tipos de datos.

Un tipo de datos se dice polimorfo si es un tipo de datos generalizado o no completamente especificado. Por ejemplo, una lista cuyos elementos son de cualquier tipo.

Polimorfismo Ad-hoc y polimorfismo paramétrico

Se llama Polimorfismo Ad-hoc a aquel en el que el número de combinaciones que pueden usarse es finito y las combinaciones deben ser definidas antes de su uso.

Se habla de polimorfismo paramétrico si es posible escribir el código sin mención específica de los tipos, de manera que el código puede ser usado con un número arbitrario de tipos.

Por ejemplo, la herencia y la sobrecarga de funciones y métodos son mecanismos que proveen polimorfismo ad-hoc.

Los lenguajes funcionales, como OCaml suelen proveer polimorfismo paramétrico.

En OOP el polimorfismo paramétrico suele denominarse programación genérica

En el siguiente ejemplo en OCaml construimos una función similar al map de Perl.

La función mymap ilustra el polimorfismo paramétrico:

la función puede ser usada con un número arbitrario de tipos, no hemos tenido que hacer ningún tipo de declaración explícita y sin embargo el uso incorrecto de los tipos es señalado como un error:

    # let rec mymap f list =
      match list with
          [] -> []
        | hd :: tail -> f hd :: mymap f tail;;
    val mymap : ('a -> 'b) -> 'a list -> 'b list = <fun>
    # mymap (function  n -> n*2) [1;3;5];;
    - : int list = [2; 6; 10]
    # mymap (function  n -> n.[0]) ["hola"; "mundo"];;
    - : char list = ['h'; 'm']
    # mymap (function  n -> n*2) ["hola"; "mundo"];;
    This expression has type string but is here used with type int

En los apuntes del profesor en Análisis de Tipos de Funciones Polimorfas (opens in a new tab) se muestra un pequeño lenguaje que permite el polimorfismo paramétrico. Está escrito en Perl usando Eyapp. Esta es la gramática Eyapp basada en la sección A language with Polymorphic functions del libro de Aho, Sethi y Ullman, 1986, p. 367:

  p: d <+ ';'> '{' e <%name EXPS + ';'> '}'
  ;
 
  d: id ':' t
  ;
 
  t:  INT
    | STRING
    | TYPEVAR
    | LIST '(' t ')'
    | t '*' t
    | t '->' t
    | '(' t ')'
  ;
 
  e:  id '(' optargs ')'
    | id
  ;
 
  optargs:
      /* empty */
    | args
  ;
 
  args: e
     | args ',' e
  ;
 
  id: ID
  ;

Y este es un ejemplo de programa conforme a la gramática Eyapp anterior:

pl@nereida:~/doc/casiano/PLBOOK/PLBOOK/code/Aho-Polymorphism/lib/Aho/script$ \
                                                         cat -n prueba01.ply
1  first :  list(ALPHA) -> ALPHA;
2  q : list(list(int))
3  {
4    first(first(q))
5  }

Equivalencia de Expresiones de Tipo

La introducción de nombres para las expresiones de tipo introduce una ambiguedad en la interpretación de la equivalencia de tipos. Por ejemplo, dado el código:

                     typedef int v10[10];
                     v10 a;
                     int b[10];

¿Se considera que a y b tienen tipos compatibles?

Equivalencia de tipos estructural y equivalencia de tipos nominal

Si utilizamos la opción de sustituir los nombres por sus definiciones y permitimos en la definición de tipo el uso de nombres de tipo no declarados se pueden producir ciclos en el grafo de tipos.

Por ejemplo, el siguiente programa:

    nereida:~/src/perl/testing> cat -n typeequiv.c
      1  #include <stdio.h>
      2
      3  typedef struct {
      4     int x, y;
      5     struct record *next;
      6  } record;
      7
      8  record z,w;
      9
     10  struct recordcopy {
     11     int x, y;
     12     struct recordcopy *next;
     13  } r,k;
     14
     15
     16  main() {
     17    k = r; /* no produce error */
     18    z = w; /* no produce error */
     19    r = z;
     20  }

Produce el siguiente mensaje de error:

    nereida:~/src/perl/testing> gcc -fsyntax-only typeequiv.c
    typeequiv.c: En la función 'main':
    typeequiv.c:19: error: tipos incompatibles en la asignación

En lenguajes dinámicos una forma habitual de equivalencia de tipos es el tipado pato:

Duck typing

Se denomina duck typing o tipado pato a una forma de tipado dinámico en la que el conjunto de métodos y propiedades del objeto determinan la validez de su uso. Esto es:

dos objetos pertenecen al mismo tipo-pato si implementan/soportan la misma interfaz independientemente de si tienen o no una relación en la jerarquía de herencia.

El término hace referencia al llamado test del pato: If it waddles like a duck, and quacks like a duck, it's a duck!.

Conversión de Tipos

El comprobador de tipos modifica el árbol sintáctico para introducir donde sean necesarias. Por ejemplo, si tenemos

    int i;
    float x;
 
    x+i;

Dado el árbol de la expresión PLUS(VAR, VAR), el analizador de tipos introducirá un nodo intermedio INT2FLOAT para indicar la necesidad de la conversión y especificará el tipo de PLUS que se usa:

PLUSFLOAT(VAR, INT2FLOAT(VAR)).

Una transformación árbol de optimización que entra en este punto es la conversión de tipo en tiempo de compilación de las constantes. Por ejemplo, dados los dos programas:

     float X[N];               float X[N];          
     int i;                    int i;               
                                                    
     for(i=0; i<N; i++) {      for(i=0; i<N; i++) { 
       X[i] = 1;                 X[i] = 1.0;        
     }                         }                    

los efectos sobre el rendimiento serán lamentables si el compilador no realiza la conversión de la constante entera 1 del programa de la izquierda en tiempo de compilación sino que la conversión se deja a una subrutina de conversión que es llamada en tiempo de ejecución. En tal caso se obtendrían rendimientos completamente diferentes para los programas en la izquierda y en la derecha.

Referencias

• Apuntes del Profesor sobre Análisis de Tipos (opens in a new tab). 2000-2012.